Nonexistent Lifestyles

Andy Towle, in reference to the recent story (see, for example, here) about Hallmark's introducing greeting cards that celebrate same-sex marriage, quotes a reactionary "family values" group promoting their own boycott of Hallmark as saying

Let them know you do not appreciate Hallmark promoting a lifestyle which is illegal in 48 states.

Now, aside from their casually dissing the gerund, what's wrong with this statement?

Clue: it's an ontological problem. It reminds me of a discussion I had at a party once about whether Catholic priests can be married. It turns out to verge on the trick question unless one is already in a pedantically scholastic mood–as I was at the time. The answer, of course, is that Catholic priests may be in a state of marriage, but they may not enter into a state of marriage. (This is how it is that Catholic priests who were formerly Episcopal priests may have canonically legal spouses.)

Although same-sex couples are technically prohibited in a large number of states from being married, the actual implementation of this prohibition occurs at the permission-to-marry (or permission "to gay marry", as Arnold Zwicky says is fast becoming current) stage through the denial of legal marriage licenses.

Thus we discover that although same-sex couples are technically prohibited from being gay married, in fact we have no choice because we cannot become gay married to being with.

And so I find it odd, this complaint about an "illegal lifestyle" that, where it is illegal, is an entirely nonexistent lifestyle.

Posted on August 23, 2008 at 20.32 by jns · Permalink · 2 Comments
In: All, Faaabulosity, Such Language!

"Waking Up Bear"

A couple of days ago in the mail I got my two contributors' copies of the new anthology Bears, edited by Richard Labonté (Cleis Press, August 2008). Before you order your copy I'll remind you that this anthology is a collection of gay erotica, and the subject is bearish men, about whom I like to write, as you may know by now.

My story (by my fictional self Jay Neal, of course) is called "Waking Up Bear", which also happens to be one of my favorite titles. As I described it on Jay Neal's website:

Stephen and Barry have been together for over a decade without major drama, until one day Barry wakes up to find out that he's turned–overnight!–into a bear. Major drama ensues, but life returns to domestic tranquility through the agency of bear-spiritualist Onslo Bigpaw.

It seems almost a miracle to me that this story ever saw the light of publication since it is itself a drama that has stretched over at least the last six years.

Sometime in 2002 or 2003 I had the beginning idea: a pair of buffed, suburban A-gays live a peaceful existence until one wakes up one morning, inexplicably transformed into something husky and hairy exceeding his worst nightmare about not going to the gym. It had good potential to examine some interesting relationship issues, social stereotypes, and indulge in a bit of humor, too.

Rather quickly I wrote the first 1,000 words of a planned 3,000 or so. Then I stalled. I got Barry and Stephen to a certain point (the breakfast table) and then I had no idea what happened next. Absolutely no idea. Well, I had some ideas but they were all worse than awful, or maudlin, or trivial and uninteresting.

And there they sat, 1,000 lonely words, for something like 3 years. At intervals, maybe once a month, I gave the situation some thought but how to continue eluded me.

Then came that interesting and productive time in December, 2005 when I was mostly confined to the living room couch, recovering from my broken leg. Around 2 or 3 in the morning, when the house got very quiet, I could hear the muses whispering. In one period of about 2 weeks I wrote 5 stories (for a total of some 15,000 words). One of those was the ending of "Waking Up Bear"

In an earlier story I had introduced a character I'd become fond of: Onslo Bigpaw,* and he turned out to be the character to help me end the story. His card reads

Onslo Bigpaw
Bear Psychic & Spiritual Healer
“Why Settle for a Medium
when you could have an Extra-Large”

Finished at last! In 2007 I saw a "call for submissions" for an anthology in preparation that was to be a collection of bear stories with supernatural elements. What better place! I sent the story along. After not too long I heard from the editor, who said he liked the story but it was more sexual than he'd wanted, would I consider changing it?

Thus, it seemed, I had returned to the story that would never end, but it didn't happen that way. I thought for a short while and came up with an idea for a delightfully romantic but still relevant ending to the story, so I rewrote the final 2,000 words or so and sent it back to the editor. I never heard from him again.

Well, these things happen. So here I had this story that for years I could not find the ending and now it had two. At the beginning of this year I took both of them out again and looked critically to try to identify what I thought were the strongest parts of both versions, and then I retained those elements, merging them and rewriting what came after that first 1,000 words, ending up now with a third version and something closer to 5,000 words.

And then I heard that Richard was putting together this Bears anthology and, for various reasons, had to do it on rather short notice. Did I have something? Well, yes, it just so happened….

And so "Waking Up Bear" finally has a final form. I am relieved.
———-
*Yes, I chose the name "Onslo" in conscious homage to Hyacinth Bucket's brother-in-law. [Yes, I've updated the next day the spelling of Hyacinth's last name to make it correct. I can't believe I got it wrong the first time. It must be time for me to review "Keeping Up Appearances".]

Posted on August 22, 2008 at 00.17 by jns · Permalink · One Comment
In: All, Personal Notebook, Writing

Ennuyeuse

Matthew Guerrieri was writing about the reasons for the relative popularity of avant-garde painting over avant-garde music. It seems an interesting essay that I'll finish later because that's not the point right now.

Near the beginning he quotes fellow art critic Charles Baudelaire (i.e., the Baudelaire) on the superiority of painting to sculpture. Again, it's interesting but all I'm after here is this bit:

Baudelaire made his initial splash as an art critic; in a long essay reviewing the Paris Salon of 1846, he rather infamously included a section explaining "Pourquoi la sculpture est ennuyeuse"—why sculpture is boring.

[Matthew Guerrieri, "Thermostat", Soho the Dog, 19 August 2008.]

"Ennuyeuse"! What a lovely and useful word.

This may become my new favorite French word, although it does have to compete with grenouille, which was my French teacher's favorite decades ago, and floconeuse, which we saw a few years ago on the bilingual packaging for an ice-crushing machine. They're both terrifically fun to pronounce, but ennuyeuse also seems eminently useful.

Posted on August 21, 2008 at 17.22 by jns · Permalink · Leave a comment
In: All, Briefly Noted, Such Language!

Loud, but Honest

From the National Portrait Gallery, "Amy Henderson, a historian at the National Portrait Gallery, discusses Ethel Merman, and her 1971 portrait by artist Rosemarie Sloat. The portrait is currently on view at NPG, in the 'Bravo!' exhibition, on the museum’s third floor mezzanine." It's an iconic portrait of Merman as Annie Oakley in Annie Get Your Gun. it's an amazing portrait, too; looking at it just sounds like Merman.

Ms. Henderson had some amusing anecdotes to relate. I particularly liked this bit:

It was the same voice that had catapulted her to overnight stardom in the Gershwins’ 1930 Broadway musical, Girl Crazy. When she sang “I Got Rhythm” on opening night, she stopped the show: “I held a high C note for sixteen bars while the orchestra played the melodic line—a big, tooty thing—against the note. By the time I’d held that note for four bars the audience was applauding. . . .” They kept applauding, and she did several encores. “When I finished that song,” she recalled, “a star had been born. Me.”

Her vibrant personality and clarion voice reverberated through Broadway’s greatest years, and America’s leading composers adored her. Cole Porter once said, “I’d rather write songs for Ethel Merman than anyone else in the world,” and songwriters from the Gershwins to Stephen Sondheim and Jule Styne agreed. Merman thought it was because she was always true to the lyrics—“I sing honest. Loud, but honest.”

[Amy Henderson excerpt from Deborah Sisum, "Ethel Merman: Queen of the American Musical Stage", National Portrait Gallery, 14 August 2008.]

I think I can find a place for that phrase "a big, tooty thing"!

But I liked most this Merman self-assessment: "I sing honest. Loud, but honest." That would be it, I think.

Posted on August 21, 2008 at 17.06 by jns · Permalink · Leave a comment
In: All, Common-Place Book, Music & Art

Coy Coroners in Crime Thrillers

I am reading a crime thriller that I'm rather enjoying (Giles Blunt, Black Fly Season); it's the second of his that I've read and so far and he suits my taste. It's got elements of police procedural to it: the central recurring characters are police detectives working in the fictional northern-Ontario town of Algonquin Bay.

This also means that when bodies are discovered we get to see some police procedure in action, the scene-of-crime people get called out, people in bunny suits search for forensic evidence, and there's always a coroner who shows up to certify death. These coroner characters are almost universally made into the comic relief through their strange personalities, inappropriate senses of humor, or other colorful characteristics.

But now we come to the bit that makes me peevish. In every book of this type that I read the coroner shows up and starts looking at the body. The coroner pronounces the body dead and makes a "preliminary assessment" that the smashed in skull ("trauma with blunt instrument") or the gaping hole in the chest ('apparent gun-shot wound") probably was involved and may even have led to death.

Then, as if on cue, the impatient detective says something like "What can you tell me about the time of death, Doc?" There ensues a conversation that invariably runs along these lines:

"What can you tell me about the time of death, Doc?"

"You know I can't say anything definite about that. There are so many variables to consider. It's been cold out lately. This is a wet location…. Maybe we'll know more once we get him/her on the table."

"Sure, sure, but can't you give me something?"

"Nothing you can use in court, of course."

"Just a rough estimate will help. Anything. I won't hold you to it."

"Off the record I'd say, oh, he/she's been dead

  • five-and-a-half hours
  • 24 to 36 hours
  • a good 5 days

give or take a few hours, of course."

Has neither of these people ever read one of these novels? Why must the coy coroner wait to be asked every bloody time by the detective and then demur for some many paragraphs?

Okay, I realize that this is the one chance (or maybe not, since there will usually be two or more bodies before the book ends and the coroner will get to repeat his/her reluctance to the detective, although if there are three bodies or more chances are there will appear at least two coroners, a second to provide comic relief from the comic relief of the first and to allow the author to go through the entire catechism again with a different character) for the author to fill up a page or two with amusing dialog before the minor character of the coroner leaves the stage.

But still. Is this realistic at this point? Is there a coroner alive–even within the pages of a crime thriller–who doesn't know that "time of death" is the first thing the impatient detective is going to ask about?

Posted on August 21, 2008 at 16.27 by jns · Permalink · One Comment
In: Crime Fiction, Feeling Peevish

Beard of the Week XLV: Work Makes Heat

This week's impressive beard belongs to British physicist James Prescott Joule (1818-1889), the same Joule who gave his name (posthumously) to the SI unit for energy. Wikipedia's article on Joule and his most noted contribution to physics is admirably succinct:

Joule studied the nature of heat, and discovered its relationship to mechanical work (see energy). This led to the theory of conservation of energy, which led to the development of the first law of thermodynamics.

At the time that Joule was doing his work, heat was still thought to be caused by the presence of the substance "caloric": when caloric flowed, heat flowed. That idea was coming under strain thanks largely to new experiments with electricity and motors and observations that electricity passing through conductors caused the conductors to heat up, a notion that proved incompatible with the theory of caloric. This was also still early days in the development of thermodynamics and ideas about heat, work, energy, and entropy had not yet settled down into canon law.

Joule found that there was a relationship between mechanical work (in essence, moving things around takes work) and heat, and then he measured how much work made how much heat, a key scientific step. His experiment was conceptually quite simple: a paddle in a bucket of water was made to turn thanks to a weight falling under the influence of gravity from a fixed height. As a result the water heated up a tiny bit. Measure the increase in temperature of the water (with a thermometer) and relate it to the work done by gravity on the weight (calculated by knowing the initial height of the weight above the floor).

In practice, not surprisingly, it was a very challenging experiment.* The temperature increase was not large, so to measure it accurately took great care, and Joule needed to isolate the water from temperature changes surrounding the water container, which needed insulation. Practical problems abounded but Joule worked out the difficulties over several years and created a beautiful demonstration experiment. He reported his final results in Cambridge, at a meeting of the British Association, in 1845.

Joule's experiment is one of the ten discussed at some length in George Johnson, The Ten Most Beautiful Experiments (New York : Alfred A. Knopf, 2008, 192 pages), a book I recently finished reading and which I wrote about in this book note. It was a nice book, very digestible, not too technical, meant to present some interesting and influential ideas to a general audience, ideas that got their shape in experiments. Taken together the 10 essays also give some notion of what "beauty" in a scientific experiment might mean; it's a notion intuitively understood by working scientists but probably unfamiliar to most nonscientists.
__________
* You knew that would be the case because people typically don't get major SI units named after them for having done simple experiments.

Posted on August 18, 2008 at 03.00 by jns · Permalink · One Comment
In: All, Beard of the Week

The Majestic Unity of the Natural World

Awhile back I was doing my lunchtime reading in the very interesting book The two-mile time machine : ice cores, abrupt climate change, and our future, by Richard B. Alley. In short, the book is about deep ice cores taken from the ice cap in Greenland and the incredible amount of information they give us about climate in ancient and prehistoric times and then expands on all matter of topics impinging on paleoclimatology, a word that just sounds cool to me (no pun intended). I loved the book and recommend it highly for a number of reasons; my book note is here. Overall the book is a careful and considered look at the history of climate change and the potential for humans to affect it.

I marveled. Even though I am a scientist and I'm accustomed to a naturalistic and reductionist view of the natural world, it is still incredible sometimes to see just how well amazingly intricate and lengthy deductions about how nature must operate actually do work together, fitting one to another like the most precise gears to make a clockwork mechanism of surprising accuracy and precision.

Detractors of science and those who lob in their bizarre "theories" from the fringe usually do not appreciate that new scientific theories are exceedingly constrained things. Any new theory not only has to provide an explanation for some new and troublesome observation, but it has to explain everything in its domain that was explained by the theory it replaces, and it must coexist harmoniously with the very large number of existing theories that surround it in the system of science. That's rarely an easy task.

So I marveled. From those two-mile long ice cores flowed an amazing amount of intricate analyses and consequent deductions about the history of climate before there were humans to record it–or even think of recording it. One could look at the layers of the ice core like tree rings–and fit some of those observations with tree-ring timing. They could tell how much snow fell. They could measure the conductivity of sections of the ice core. They could analyze the relative abundance of gases at various times by actually measuring tiny bubbles of air trapped in the ice. Mass spectroscopy told them about the relative abundance of heavy water and how it varied in the past 100,000 years.

Ah, but that's just the beginning. From some of those observations they first had to build a reliable way of measuring time, answering the question: how old is a particular layer of ice core? Deductions there had to give a consistent picture with every other dating technique it could be made to line up with. Then one could start to build a picture of what the climate was doing, and every deduction was made in a milieu of other deductions and existing scientific knowledge so that everything cohered.

Accomplishing that is an amazing feat although it is what science does all the time. Every bit of scientific theory and observational data is continually subjected to a barrage of attacks from all sides probing for any inconsistency with existing knowledge. It's a remarkable process, but it's maybe even more remarkable that it works at all. That may be the crowning achievement of science.

Of course, the mystery is that it is even possible to create such a coherent whole. This, of course, is the point Einstein was making when he said "The most incomprehensible thing about the universe is that it is comprehensible."*

While pondering this great mystery I had a brief moment–a very brief moment–of feeling sorry for people like young-earth creationists and "intelligent-design" creationists, a group that is rarely the object of my pity. But think for a moment on these pitiable ones and all others whose core belief is that their god created all the details of the universe that they can see and the explanation for all of it is "god did it that way".

Young-earthers see–must see–"nature" as a capricious trickster with, for example, fossils laid down according to the whim of their creator and thus allowing no meaningful patterns to be observed, no deductions to be made, no connections to any other physical phenomenon save through the arbitrary hand of their creator. There is no sense that observations must make a coherent whole, nor that historic puzzle pieces have to fit together into any sort of comprehensible, indisputable larger picture.

What poverty of thought that is, what a barren wasteland, an infinity of random and unconnected details about the world that need make no sense. Is this not a recipe for confusion, a path to alienation and despair? How can one move through a world, an existence, where anything is free to change from moment to moment, where nothing can be expected to be predictable, let alone understandable?

For me, nothing rivals the majestic unity of the natural world.
__________
* [note added 25 august 2008] Or maybe it was this version that Richard Dawkins attributes to J.B.S. Haldane that I was mentally grasping at: "Now, my own suspicion is that the universe is not only queerer than we suppose, but queerer than we can suppose. I suspect that there are more things in heaven and earth than are dreamed of, or can be dreamed of, in any philosophy."

Posted on August 15, 2008 at 21.44 by jns · Permalink · 2 Comments
In: All, Books, It's Only Rocket Science, Reflections

Beard of the Week XLIV: Infinity and Beyond


This week's beard belongs to Georg Cantor (1845–1918), the German mathematician who advanced set theory into the infinite with his discovery/invention of transfinite arithmetic. Why I hedge over "discovery" or "invention" we'll get to in a moment.

I first encountered Cantor's ideas in college in my course of "mathematical analysis", which was largely concerned with number theory. I remember the stuff we worked on as beautiful but nearly inscrutable, and very dense: our textbook was less than an inch thick but the pages were dark with mathematical symbols, abbreviations, and shorthand, so that a semester was much too short a time to get through the whole thing.

Cantor proved a series of amazing things. First, consider the positive integers (or natural numbers, or whole numbers, or counting numbers): 1, 2, 3, 4, etc. We know that there is no largest integer because, if there were, we could add 1 to it to get one larger. Therefore, the set of positive whole numbers is infinite. This is also described as a countable, or denumerable infinity, because the elements of the set can be put into a one-to-one correspondence with the counting numbers–a rather obvious result because they are the counting numbers and can thus be counted. Think of counting and one-to-one correspondence for a bit and is becomes obvious (as the textbooks are wont to say) that the set of positive and negative integers (…,-3, -2, -1, 0, 1, 2, 3, …) is also a countable infinity, i.e., there are just as many positive and negative integers as there are positive ones. (This is transfinite arithmetic we're talking about here, so stay alert.)

Next to consider is the infinity of rational numbers, or those numbers that can be written as the ratio of two whole numbers, i.e., fractions. How infinite are they compared to the whole numbers?

Cantor proved that the cardinality of the rational numbers is the same as that of the whole numbers, that the rational numbers are also denumerable. For his proof he constructed a system of one-to-one correspondence between the whole numbers and the rationals by showing how all of the rational numbers (fractions) could be put into an order and, hence, counted. (The illustration at the top of this page shows how the rationals can be ordered without leaving any out.)

Any set whose elements can be put into a one-to-one correspondence with the whole numbers, i.e., that can be counted, contains a countable infinity of elements. Cantor gave a symbol to this size, or cardinality, or infinity, calling it 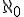\aleph_0 (said "aleph nought"), using the first letter of the Hebrew alphabet, named "aleph".

Then there are the irrational numbers, numbers that cannot be written as ratios of whole numbers. The square root of 2 is a famous example; discovery of its irrationality is said to have caused great consternation among Pythagoreans in ancient times. There are several interesting classes of irrational numbers, but for this consideration it is enough to say that irrational numbers have decimal expansions that never terminate and whose digits never repeat. 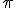\pi, the ratio of the circumference to the diameter of a circle is a famous irrational number and many people are fascinated by its never ending decimal representation.

Cantor proved that the cardinality of the real numbers (rational and irrationals put together) is greater than 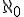\aleph_0 — they cannot be counted. He proved this with his diagonalization technique, in which he showed that no matter how many rational numbers were packed into an interval one more could always be constructed that was not in that set.* (For the proof, see this Wikipedia page; it's not a difficult proof to read but it takes a clear head to understand it.)

Cantor referred to the real numbers as the continuum because it was so dense with numbers. Cantor had shown that the cardinality of the continuum was strictly larger than the cardinality of the whole numbers. Now we have two sizes of infinity, if you will! There are more, but we'll stop there.

Cantor was haunted by being unable to prove something he believed to be true, known as the "continuum hypothesis". In words the conjecture is that there is no cardinality of infinity between the cardinality of the countable infinity and the cardinality of the real numbers. When he'd reached this stage Cantor's mental health faced severe challenges and he became obsessed with trying to prove that Francis Bacon wrote the plays of Shakespeare. A decade after Cantor died Kurt Gödel proved that the Continuum Hypothesis was a formally undecidable proposition of set theory, that it could neither be proved or disproved.

Much of this story appeared in one book I finished recently: Amir D Aczel, The Mystery of the Aleph : Mathematics, the Kabbalah, and the Search for Infinity (New York : Four Walls Eight Windows, 2000, 258 pages). My book note is here.

Just after that book I finished another book on a mathematical topic: Mario Livio, The Golden Ratio : The Story of Phi, The World's Most Astonishing Number (New York : Broadway Books, 2002, viii + 294 pages). Its book note is here.

Aside from their interest in mathematical topics, the two books have very little in common with one exception: both authors ruminated on the question whether mathematics is created or discovered, whether the great edifice exists only in the minds of humans or whether it somehow has an independent existence in the universe independent of the human mind. The complication to the question of course is the remarkable utility of mathematics when it comes to explaining how the universe works.

I once had a long-time debate with my roommate in graduate school on the question. I remember winning the debate after months, but I forget which side I argued. It's the sort of thing that physics and philosophy graduate students argue about.

Oddly to me, aside from the vague coincidence that two books I should read back-to-back considered this question,† is that each author felt very strongly about the answer to the question, feeling that his answer was the obvious best choice, but, as you've guessed, one believed that mathematics was obviously discovered and the other felt that mathematics was clearly invented.

Even as I once argued that mathematics was obviously discovered, I realized from reading these two authors' discussions that I now pretty much would go with the conclusion that mathematics is an invention of the human mind. Now, how that could be and still have mathematics accord so well with the operating of the universe is a question that I'm afraid goes well beyond the scope of this already too long posting.

Besides, the hour grows late and my mind lacks the clarity to be convincing right now. So, as a distraction, I leave you thinking about the much simpler question of how one type of infinity can be larger than another.
__________
* Think very carefully about the distinction between not being able to think of a way to count the set versus proving that there is no way it can be done.

† Not so surprising, really, if you consider the fact that when I'm browsing for books on the library stacks I'll frequently find more than one on a single shelf that looks interesting.

Posted on August 11, 2008 at 01.27 by jns · Permalink · Leave a comment
In: All, Beard of the Week, It's Only Rocket Science

From the Pad I

By the reclining chair from which I watch movies on our television set I keep a pad of paper. Occasionally someone in one of the visual treats we are enjoying will say something that I think worth making a note of, so I write it on the pad. Many months later I notice that I have a small page of quotations that I wish to preserve but written on a sheet of physical paper that I'd as soon throw away.

It's your lucky day!

From an episode of one of Sister Wendy Beckett's televised series on art ("Sister Wendy's Grand Tour" seems most likely but I can't say for sure–we've enjoyed them all), these two snippets:

I'm besotted with Klee!

When is conceptual art great art? When it produces an image that is visually satisfying.

And now, another two quotations, these from the movie "The Prime of Miss Jean Brodie", an outstanding film based on the outstanding novel by Muriel Spark that we must have watched at about the same time as the Sister Wendy presentation since these notes were on adjacent sheets. I imagine that both of these came out of the mouth of Maggie Smith in her unforgettable portrayal of Miss Jean Brodie, who was in her prime.

She thinks to intimidate me by the use of quarter hours.

Mr. Lowther, the philistines are upon us!

Posted on August 10, 2008 at 00.21 by jns · Permalink · Leave a comment
In: All, Common-Place Book

Remembering a Story

A week ago I finished a short story, the first fiction I'd written since my father died late last December. The story is called "The Last Night at Nan's Han-N-Egger". Oddly, for me at least, there are no gay men in the story (so far as we know) and there is no sex. There is a bit of violence and an off-stage possible murder. Evidently this is my first story in a crime genre. In large measure the story came out as I had hoped it would, and it seems to elicit the type of response from its readers that I had planned.

In fact the story seemed to end up having a rather vivid presence for me and I am still seeing bits of scenes from it. Creating a vivid, uninterrupted dream in the mind of the reader is my primary responsibility as the author, at least according to my favorite fiction theorist John Gardner (see his The Art of Fiction); we'll talk more about that someday. The stories I think my best are the ones that have for me a vivid presence, usually because I know a great deal about the characters, but I don't always know whether that effect is shared with my readers. If it's vivid for me is it vivid for them? Often, I suspect, but not always perhaps.

Creating the vivid dream takes time and effort, and doing it with enough detail and vividness feels to me a lot like remembering the events of the story; thinking up the story and working out its details feels like trying to remember every detail about what happened even though, of course, none of it's actually happened. So far as I can tell this remembering work goes on prior to any of the actual writing, by which I mean that it precedes the writing down of words one after the other that are meant to convey to readers the story that I have remembered.

If all goes well I am able to choose just the right words with exactly the right economy to convey the dream into the memory of my readers as vividly as I remember it. Of the infinite things one can write, how I or any other author goes about choosing just the few words to do the work (in essence, a vanishingly small sampling of possible words and sentences) of conveying enough pertinent detail about the dream vividly to the reader is pretty much a mystery to me and I'm sure it presumes something about my audience. How one can overload that operation with other short-story features like themes and symbols only deepens the mystery.

My best stories–and the ones I have read, too–are populated with characters that have really "come alive". Everyone has heard numerous authors explain how it is that characters tend to take on a life of their own in stories and do whatever they damn well feel like whether it is contrary to the author's plans or not. If I needed a theory I'd suspect that characters feel so real because the story, if it reaches the vivid target, becomes like a memory and then the characters necessarily seem very real because in our memory they are indistinguishable from the memories we maintain of real people.

I'd better stop before this gets any spookier. By the way, since "The Last Night at Nan's Ham-N-Egger" was written for a more general audience than my usual, I'd like to share it with my blog friends. If you would like to read it, leave a comment (with email address, please!) and I'll send a copy in email.

Posted on August 9, 2008 at 19.21 by jns · Permalink · 4 Comments
In: All, Writing

Byzantine Style in Commercial Art

The apse mosaic at the church of St. Paul's Outside the Walls, near Rome, Italy, is a gorgeous work of Byzantine style art. Here is a photograph Isaac took of the central figure of Christ, shown in a variant of his portrayal as "Christ Pantocrator". Near the Christ's right foot is a small, white thing looking rather like a hermit crab. Closer inspection reveals that it is actually a portrait of Pope Honorius III being very, very humble.

We recognize this convention in art of portraying the donors (or other supplicants) of religious paintings with portraits within the painting itself, but usually as very small people, being a graphic representation of their relative importance to the other figures portrayed. We recognize it but most modern viewers seem to look on it as something affected, something silly and very old fashioned. We moderns are much more sophisticated–we've got perspective, after all!–and our art would never do anything so ridiculous and unrealistic as portraying people or objects with relative sizes that demonstrate their relative importance.

Well, not quite. I was sitting in my usual place for luncheon, looking at the illuminated, illustrated menu board, when that thought passed through my mind and I laughed aloud.

Examine, if you will, this sign offering for sale a "Cheesy Beefy Melt Combo Meal" at a Taco Bell (a limited-time menu offering that evidently did not appeal to the taste of NYC Food Guy). It's representative of the way menu items are displayed here and on many other similar menus.

What do we see? We see the central food item, the Cheesy Beefy Melt, displayed at a large, juicy, enticing size, large enough to dominate the space alloted to portraying the combo-meal offer. But what else do we see? We see a depiction of a crunchy taco and a large drink, the ancillary food items that make the combo meal a "combo".

Oddly, it passes as so unremarkable as to be almost invisible, but please note the relative sizes of the ancillary food products. They are tiny! If the accompanying crunchy taco were as shown, it would be about a centimeter across. Likewise the "cruiser cup" for the soda is so small that it might hold as much as one cubic centimeter of soft drink.

And yet I have never seen anyone point and laugh at this depiction, nor point out how "unrealistic" it is, nor demand the tiny taco with their meal. This matter of relative-size silliness must pass totally unprocessed in people's minds, too, because there's not much that they won't ask for based on the way things appear in the picture menus, or even on what they imagine may be shown in the picture menus.

So, maybe we're not so modern and sophisticated as we think. Or, perhaps the people in earlier times were not so unsophisticated as we frequently impugn. This could, of course, be the starting observation for an essay about how painters in a Byzantine style merely had other priorities in their depictions of "reality" and that they found their portrayals quite realistic and life-like, not unsophisticated and primitive. Those latter ideas merely result from changes in perception and priorities in visual representation as they accord with reality.

Posted on August 8, 2008 at 01.07 by jns · Permalink · 2 Comments
In: All, Music & Art, Plus Ca Change...

Beard of the Week XLIII: Let's Make a Deal

This week's beard belongs to David Flannery, a lecturer in mathematics at the Cork Institute of Technology, Cork, Ireland. He is shown with his daughter Sarah Flannery, author of the book In Code : A Mathematical Journey (New York : Workman Publishers, 2001); David Flannery is listed as her coauthor.

The book is a fascinating, entertaining, and instructive one, blurbed on the jacket as "a memoir with mathematics". It's Sarah's autobiographical account of her route to winning some prestigious young scientist awards in 1998 and 1999 with a good dose of mathematical fun and really good writing about the mathematical ideas at the core of public-key cryptography, if you can imagine such a thing. I enjoyed reading it very much and I think a lot of other people might enjoy it too. Here's my book note.

Okay, so her coauthor and father happens to have a very lovely beard, but it's all just a pretext for passing along an interesting problem and its lovely solution from an appendix of the book. I'm sure this surprises no one here.

In America this statistical brain-teaser tends to be known as the "Let's Make a Deal" problem. Imagine you're playing that game. Host Monty presents you with three doors: behind one is a wonderful and expensive new car, behind the other two nothing of much value. You chose one door at random. Host Monty then opens one of the two remaining doors, revealing an item of little value.

Do you change your initial choice?

Most of us who've done some statistics are suckered into saying "no" at first because we think that the probability of our having made the correct choice has not changed. However, it has indeed changed and a more careful analysis says we should always choose the other door after Monty opens the door of his choice. One can perhaps go along with that by realizing that Monty did not choose his door at random–he knows where the car is and he chose not to reveal the car, so the information we have at our disposal to make our "random" choice has changed.

However, seeing this clearly and calculating the attendant probabilities is neither easy nor obvious–usually. I've read several solutions that typically say something like "look, it's simple, all you have to do…." and they go on to make inscrutable statements that don't clarify anything.

The answer in Flannery's book is the clearest thing I've ever read on the subject; the reasoning and calculation itself by one Erich Neuwirth is breathtaking in its transparency. From "Appendix B: Answers to Miscellaneous Questions", this is her complete response to the question "Should you switch?"

Yes. In order to think clearly about the problem get someone to help you simulate the game show with three mugs (to act as the doors) and a matchstick (to act as the car). Close your eyes and get your helper to hide the matchstick under one of the mugs at random. Then open your eyes, choose a mug and let your helper reveal a mug with nothing under it. Play this game many times, and count how often you win by not switching and how often by switching.

The following explanation of the answer "Yes, you should switch" is from Erich Neuwirth of Bad Voeslau, Austria, and appears on page 369 of the Mathematical Association of America's The College Mathematics Journal, vol. 30, no. 5, November 1999:

"Imagine two players, the first one always staying with the selected door and the second one always switching. Then, in each game, exactly one of them wins. Since the winning probability for the strategy "Don't switch" is 1/3, the winning probability for the second one is 2/3, and therefore switching is the way to go." [pp. 302–303]

Do you see the reason? Because one player always wins, the individual probabilities of each player's winning must add up to 1. The probability of a win for the "Don't switch" player is obviously 1/3 (1 of 3 doors chosen at random), so the probability of a win for the "Always switch" player must be 1 – 1/3 = 2/3. Brilliant!

Posted on August 4, 2008 at 03.00 by jns · Permalink · One Comment
In: All, Beard of the Week, Books

An Easement in Gross

We have a friend who has just finished taking her Maryland Bar Exam (congratulations, Nina!), which really more significantly she's finished studying for and worrying about taking the Maryland Bar Exam. Among her list of interesting and amusing take aways from the experience, she lists this item:

I could [sic] care less about the difference between an easement in gross and a license. Because they have the same effect.

As her husband will realize, I look forward to the chance at a party (to happen tomorrow) celebrating the occasion to interrogate her on what exactly the operational differences are between a "license" and "an easement in gross".

If there is absolutely none, of course I'd use "easement in gross" in preference to "license" just because it sounds more provocative and less scrutable.

Posted on August 1, 2008 at 19.37 by jns · Permalink · 2 Comments
In: All, The Art of Conversation

All Pleasure is a Risk

Isaac asked me to post this where we could find it easily, since it is these days frequently referenced in conversation. This little sign seems to have great predictive powers, eliciting gratifying responses–or non-responses–from people we find more fun to be around–or less so.



[via Arnold Zwicky at Language Log ("Today's little amuse-bouche") whose attention was drawn to it by Chris Ambidge, friend of this blog and Beard of the Week Emeritus.]

In case the text of the sign in the photograph is not legible to you, it reads

Keep back from the platform edge
or you may get sucked off

Posted on August 1, 2008 at 16.55 by jns · Permalink · Leave a comment
In: All, Laughing Matters, Raised Eyebrows Dept.

Marriage Still More Equal

I still feel the excitement, particularly since we live much closer to Massachusetts than to California, being on the right coast of the US. Anyway, you may recall that same-sex marriage, although legal in Massachusetts, was restricted to those couples for whom marriage would be legal in their home states. This was a parting gift from the former governor whose name need not be mentioned here since it will sink into the mud of history.

The barrier was a law passed in 1913 to help prevent miscegenation in that state. Recently there was a surge of interest in the Massachusetts legislature to repeal that law, they did it, and today the governor signed the repeal.

The apparent reason for this sudden breakthrough is economic jealousy of California, the arriviste of marriage equality where out-of-state couples where not barred from getting legally married and spending lots of money in that state. As reported in the article linked above

A state study estimates that more than 30,000 out-of-state gay couples – most of them from New York – will wed in Massachusetts over the next three years. That would boost the state’s economy by $111 million and create 330 jobs, the study estimated.

Word is spreading among fiscally sensitive officials in other states that there's good money to be had in marriage equality to those who get there first.

Isn't it a good bit of fun if the impetus for widespread adoption of marriage equality happens sooner than conservatives would like because of the economic hard times caused by Republican "economic theories" of wealth redistribution to the already wealthy?

Posted on July 31, 2008 at 23.11 by jns · Permalink · Leave a comment
In: All, Faaabulosity

On A Bus, Irregularly

It's not something that happens regularly on a bus.

— RCMP Staff Sgt. Steve Colwell at a news conference, talking about a gruesome incident on a Greyhound bus from Edmonton to Winnepeg in which a man apparently stabbed to death and then beheaded his seat partner

[source]

Posted on July 31, 2008 at 22.50 by jns · Permalink · Leave a comment
In: All, Briefly Noted

A Summer Menu II

This week's dinner party was a more casual affair so I went with a more casual arrangement of dishes, what I've come to think of as a "salad menu".

I have to admit that I was a bit disappointed in the pork loin; it was perfectly edible but I wanted something more scrumptious. However, I usually have some sort of issue with pork loin, so maybe it's not my best choice. It was on sale though….

The oven roasted potatoes were the same preparation as I gave the recipe for last time and they came out yummy again and disappeared fast. This time I was smart enough to make the entire 5-pound bag and I think we ate most of them. This time I used Red Bliss potatoes; last time it was White Russets. Both were fine but Isaac and I both gave a slight edge to the Russets, which seemed to crisp a little better.

Brandy Alexanders are perhaps the best cocktail mixture ever created. They are absolutely yummy but one can easily think them less potent than they are.

I was trying out a recipe for cucumbers in sour cream, hoping for something that came close to the "cucumber slaw" that I've had in Lancaster County, Pennsylvania, presumably a Pennsylvania Dutch dish. This version was okay but not yet perfect, so I'll let you know when I find the right preparation.

I use the traditional recipe for Waldorf Salad in preference to any number of gussied-up versions: apples, celery, walnuts, & grapes mixed with mayonnaise. Crisp apples work best but suit your taste, and I use whatever seedless grapes I find. Dice the apples, cut the grapes in half, and coarsely chop the walnuts. The mayonnaise can most certainly come from a jar, but use one that tastes good. Waldorf Salad is a classic concoction that is almost always appropriate and tasty, but people don't often think to make it (and over dinner we always talk about the episode of "Fawlty Towers" in which a Waldorf Salad figured prominently).

The orange-orange Jell-O I made with two small packets of orange, sugar-free Jello-O, 1 cup of hot water, and 3 cups of sugar-free orange soda. The [imitation] orange flavor is intense, and the bubbles from the soda give a tiny fizz on the tongue.

But the unexpected stand-out from this menu was the Sweet-and-Sour Beet Salad. Simple and yummy and it appealed to the beet lovers and the beet less-than-lovers at the table.

— Brandy Alexander —

Mix equal parts

in a cocktail shaker with ice and shake vigorously. Strain out ice and serve in a cocktail (martini) glass.

— Sweet-and-Sour Beet Salad —

Drain the beets, reserving 1/2 cup of the beet's packing liquid.

Cut the beets into matchsticks. Combine with the red onion in a mixing bowl.

Heat the beet juice in a small saucepan along with the Splenda and the mustard, until the Splenda is dissolved. Add the vinegar, bring to a boil then turn off the heat.

Let the dressing cool some then pour over the beets and onion and stir to mix. Put it in the refrigerator to marinate for awhile, maybe a couple of hours.

[modified after "Marinated Beet Salad", originally from safeway.com]

Posted on July 26, 2008 at 00.25 by jns · Permalink · Leave a comment
In: All, Food Stuff

Personal Chocolate Cake

I am so enchanted by this concept–and ultra-simple recipe–for a personal, one-serving size, made-from-scratch-in-the-microwave recipe for chocolate cake that I'm putting a link to it here so I won't lose it before I get to try it. Y'all are free to try it, too.

It's called "Chocolate Cake in 5 Minutes!" and takes only 3 minutes in the microwave. The ingredients couldn't be simpler:

Refer to the link above for instructions with visual aids. Let me know if you try it first!

Posted on July 16, 2008 at 20.33 by jns · Permalink · 3 Comments
In: All, Curious Stuff, Food Stuff

I've Been Feeling Unreasonable Lately

The reasonable man adapts himself to the world; the unreasonable one persists in trying to adapt the world to himself. Therefore, all progress depends on the unreasonable man.
— George Bernard Shaw

Posted on July 15, 2008 at 15.52 by jns · Permalink · One Comment
In: All, Common-Place Book, Reflections

Beard of the Week XLII: The Pyramidiot

This week's beard belongs to one Charles Piazzi Smyth (1819–1900), who served as Astronomer Royal for Scotland from 1846 to 1888. That's not the reason for my interest, however. It's his pioneering work in pyramidology that I found out about today and wanted to bring to your attention. At the center of it all: the "pyramid inch".

One of the books I'm reading right now is Mario Levio's, The Golden Ratio : The Story of Phi, the World's Most Astonishing Number (New York : Broadway Books, 2002). Indeed the book is about the irrational number often denoted by the greek letter phi, and also called "the golden ratio". On page 53 & 54, in a chapter looking at what generally turn out to be crackpot theories about the ancients' use of the golden ratio in building virtually any building that has attracted the attention of mystical fantacists over the past couple hundred years, we encounter one of the more amusing: Mr. Piazzi Smyth. This brief version of the story comes from Levio's book, but there are plenty of other versions that cover the same ground with different words (e.g., the Wikipedia page for Piazzi Smyth).

First up was John Taylor who wrote a book called The Great Pyramid : Why Was It Built and Who Built It? This was well before von Daniken's ideas about aliens doing virtually everything for early people so it was assumed that the Egyptians did build them, but that they were divinely inspired: "Taylor was so convinced that the pyramid contained a variety of dimensions inspired by mathematical truths unknown to the ancient Egyptians that he concluded that its construction was the result of divine intervention."

Our author explains that, at the time, there was a popular theory that the British were the remnants of the "lost tribes of Israel" and Taylor worked out the idea that the cubit, that famous biblical unit of measure, was also the basic unit used in building the pyramids and that the cubit contained 25 "pyramid inches", which were slightly larger than the British inch. You can see where this is going: the obvious deduction, given the lost tribes of Israel thing, is that the British inch was the vestige of the pyramid inch, thus ordained by god.

Taylor's book, we're told, found great favor with Piazzi Smyth, particularly this theory about the "pyramid inch", largely because Piazzi Smyth was bitterly opposed to the introduction of the metric system in Britain. As Levio explains:

His [Piazzi Smyth's] pseudoscientific/theological logic worked something like this: The Great Pyramid was designed in inches; the mathematical properties of the pyramid show that it was constructed by divine inspiration; therefore, the inch is a God-given unit, unlike the centimeter, which was inspired 'by the wildest, most blood-thirsty and most atheistic revolution' (meaning the French Revolution).

Piazzi Smyth, by the way, wrote three very large books on the Great Pyramid in the 1860s. The first was called Our Inheritance in the Great Pyramid; the inheritance included, of course, the British inch, which he saw as a cultural and theological heirloom. Most of today's mystical and numerological nonsense about the pyramids had their origins in the works of Taylor and Piazzi Smyth.

Anyway, Levio concludes his consideration of Piazzi Smyth this way:

After reading this text [from The Great pyramid, Its Secrets and Mysteries Revealed), we cannot be too surprised to find out that author Leonard Cottrell chose to entitle the chapter on Charles Piazzi Smythin in his [1956] book The Mountains of Pharaoh "The Great Pyramidiot."

Isn't it surprising how religious crackpots tend to sound the same century after century?

Here's a bit more reading on pyramids and pyramidology:

Posted on July 14, 2008 at 23.04 by jns · Permalink · One Comment
In: All, Beard of the Week, Books, Curious Stuff