Long Ago & Far Away
In a recent comment to a post I made about reading Chet Raymo's book Walking Zero, Bill asked an interesting question:
Jeff, there's a question that has always bothered me. Raymo's talk about the Hubble Space Telescope's Ultra Deep Field image (page 174) raised it for me again. I'm sure you have the answer, or the key to the flaw in my "reasoning," such as it is. The most distant of the thousands of galaxies seen in that image is 13 billion light years away. "The light from these most distant galaxies began its journey when the universe was only 5 percent of its present age" (174-175), and presumably only a small proportion of its present size. Now, the galaxies are speeding away from each other at some incredible speed. So if it has taken 13 billion years for light to come to us from that galaxy where it was then (in relation to the point in space that would become the earth at a considerably later date), how far away must it be now? Presumably a lot farther away than it was then?
Before we talk about the universe, I do hope you noticed that the background image I used for the "Science-Book Challenge 2008" graphic, which you will see at right if you are reading this from the blog site (rather than an RSS feed), or which you can see at the other Science-Book Challenge 2008 page, is actually part of the Hubble Deep-Field image. If you follow the link you can read quite a bit about the project, which was run from the Space Telescope Science Institute (STScI), which is relatively nearby, in Baltimore. It's the science institute that was established to plan and execute the science missions for the HST; flight operations are handled at Goddard, which is even closer, in Greenbelt, Maryland.
Now let's see whether we have an answer to Bill's question.
I think you may be able to resolve the quandary if you focus on the distance of the object seen, rather than when the light through which we see it left its bounds.
The object's distance is the thing that we can determine with reasonable accuracy (and great precision) now, principally through measuring red shifts in spectra of the object.* One of astronomer Hubble's great achievements was determining that the amount of red-shift, which depends on our relative velocity, corresponds directly with the distance between us and the observed object.# So, take a spectrum, measure the red shift of the object, and you know more-or-less exactly how far away it was when the light left it.
Oh dear, but that doesn't really settle the issue, does it? On the other hand, it may be the most precise answer that you're going to get.
Saying that, when the light left the object, the universe was only 5% its current size should be seen more as a manner of speaking than a precise statement. It can be a rough estimate, along these lines. Say the universe is about 14 billion years old and this object's light is 13 billion years old, and if the universe has been expanding at a uniform rate, the the universe must have been (14-13)/14ths or about 7% its current size (which is about 5% its current size).
But I'd say you should treat that just as something that makes you say "Wow! That was a long time ago and the universe must have been a lot different", and don't try to extrapolate much more than that.
It's probably true that the universe hasn't been expanding at a uniform rate, for one thing. There's a theory that has had some following for the past 25 years, called the theory of inflation.** For reasons that have to do with the properties of matter at the extreme compression of the very, very early universe, the theory suggests that there was an "inflationary epoch" during which the universe expanded at a vastly faster rate than is visible currently. Now, some of the numbers involved are astonishing, so hold on to your seat.
The inflationary epoch is thought to have occurred at a time of about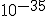 
seconds after the big bang, and to have lasted for about 
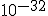seconds.## During this time, it is thought that the universe may have expanded by a factor of 
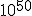. (One source points out that an original 1 centimeter, during inflation, became about 18 billion light years.)
So, inflation would rather throw a kink into the calculation, not to mention the possibility that the universe is not expanding in space, but that space itself is expanding. That can make calculations of what was where when a touch trickier.
But that's not the only problem, of course. I can hear Bill thinking, well, that may all be so, but if we're seeing the distant object as it was 18 billion light years ago, what's it doing now.
I'm afraid that's another problem that we're not going to resolve, and not for lack of desire or know-how, but because of physical limitation. The bigger, tricker issue is — and I almost hate to say it — relativity. No doubt for ages you've heard people say of relativity that it imposes a universal speed limit: the speed of light. Nothing can go faster than the speed of light. That's still true, but there's an implication that's not often spelled out: the breakdown of simultaneity, or what does it mean for thing to happen at the same time?
It's not usually a tricky question. Generally speaking, things happen at the same time if you see them happen at the same time. Suppose you repeat Galileo's famous experiment of dropping two different weights from the leaning tower of Pisa at the same time (he said he would), and you observe them hitting the ground at the same time. No real problem there: they fell right next to each other and everyone watching could see that they happened at the same time.
Suppose the objects are not next to each other though. Suppose instead that we observe some event, say, a meteor lands in your front yard. 8.3 minutes later you observe a solar flare on the sun through your telescope. "Isn't that interesting," you say, "since the Earth is 8.3 light-minutes from the Sun, that flare and my meteor's landing happened at the same time."
Well, the problem here, as you may have heard about before, is that an observer traveling past the Earth at very high speeds and using a clock to measure the time between the two events, your meteor and the solar flare, would deduce that the two events did not happen at the same time. The mathematics is not so difficult, but messy and probably not familiar. (You can see the equations at this page about Lorentz Transformations, or the page about Special Relativity.)
What happens is that in order for the speed of light to be constant in all inertial reference frames–the central tenet of special relativity–causality breaks down. Events that appear simultaneous to one observer will, in general, not appear simultaneous to another observer traveling at a uniform velocity relative to the first observer. (This cute "Visualization of Einstein's special relativity" may help a little, or it may not.) Depending on the distance between two events, different observers may not even agree on with event happened first.
So, the not-so-satisfactory answer, Bill, is a combination of 1) because of inflation, it may not be so very much further away than it was 13 billion years ago; but 2) because of the breakdown of simultaneity due to special relativity, we can't say what it's doing now anyway, because there is no "now" common to us and the object 13 billion light-years away.%
Gosh, I do hope I answered the right question!
———-
* You may recall that red shift refers to the Doppler effect with light: when objects move away from us, the apparent wavelength of their light stretches out–increases–and longer wavelengths correspond to redder colors, so the light is said to be red-shifted. This happens across the entire electromagnetic spectrum, by the way, and not just in the visible wavelengths.
# Applying Hubble's Law involves use of Hubble's Constant, which tells you how fast the expansion is occurring. The curious thing about that is that Hubble's Constant is not constant. I enjoyed reading these two pages: about Hubble's Law and Hubble's Constant. The second one is rather more technical than the first, but so what.
**Two useful discussions, the first shorter than the second: first, second.
## Yes, if you want to see how small a fraction of a second that was, type a decimal point, then type 31 zeroes, then type a "1".
% I leave for the interested reader the metaphysical question of whether this statement means that universal, simultaneous "now" does not exist, or that it is merely unknowable.
3 Responses
Subscribe to comments via RSS
Subscribe to comments via RSS
Leave a Reply
To thwart spam, comments by new people are held for moderation; give me a bit of time and your comment will show up.
I welcome comments -- even dissent -- but I will delete without notice irrelevant, rude, psychotic, or incomprehensible comments, particularly those that I deem homophobic, unless they are amusing. The same goes for commercial comments and trackbacks. Sorry, but it's my blog and my decisions are final.
on Friday, 8 February 2008 at 00.33
Permalink
Thanks, Jeff.
You said: During this time, it is thought that the universe may have expanded by a factor of 10^{50}. (One source points out that an original 1 centimeter, during inflation, became about 18 billion light years.)Given that the singularity from which the universe began is said to be a vanishingly small entity (1 cm-to-I-don't-know-how-many-powers-minus), what does a vanishingly small entity raised to 10-to-the-50th power look like? How big would it be? Bigger than a breadbox? Bigger than the solar system? Bigger than the Milky Way?
Again, you said: But that's not the only problem, of course. I can hear Bill thinking, well, that may all be so, but if we're seeing the distant object as it was 13 billion light years ago, what's it doing now. That's not really my question. My question is more, how far away from us is it now? If the universe is expanding equally in all directions, and it's now 14 times bigger than it was when the light left that 13-billion-light-year away galaxy, doesn't that put it 182 billion light years away now? I realize that's impossible, since the universe is only 14 billion years old, and I think that it would mean that light from there could never get here. So?
on Friday, 8 February 2008 at 17.38
Permalink
Along this line of thinking, it could be troublesome to think of the singularity at the origin of the universe as being an infinitely small point, i.e., a spatial singularity. It is described as a singularity because of the physical functions, mass density, temperature, other physical properties of the universe, diverge (go to infinity) at that point. That doesn't necessarily mean that spatial extent vanishes.
The universe at time zero is often pictured as small, but less commonly infinitely small, I think. However, there is ambiguity. Since it may be that space-time itself is expanding with the universe, and would have been, as a result, infinitely compacted (i.e., singular) at time zero, it simply may make no sense to ask how big the big bang thing was, but it does explain how it could be that the big bang happened "everywhere" all at once.
However, even a small thing becomes a big thing when it's magnified by a factor of 10^{50}, which is to say that it is multiplied by 10, 50 times. The example I gave was not to suggest that the original universe was a centimeter in diameter, merely that something that was the size of a centimeter, after this magnification, would be 18 billion light-years in size.
I can't find anyone to say how "big" they think the universe was at the beginning of inflation, if it makes sense to say, but I have the impression that it would generally be considered large even by that early time. Large? Well, much, much bigger than 10^{-30} light-seconds, but no answer yet on how much bigger.
How far away now? Oh, that's a tricky question. It might be 182 billion light-years away, if there were a way to measure that distance. One thing I can point out: it is a mistake to think that the edge of the universe can only be 14 billion light-years away. That's the edge of our visible universe, but an observer at the edge of our visible universe may well see that far in the other direction. Space-time itself seems to be expanding, so talking about the size of the universe beyond the merely visible is tough.
Is this close to the question? I fear that the answers will get less satisfactory as my understanding gets fuzzier and as the notions of space and time get less well-defined.
on Friday, 8 February 2008 at 18.39
Permalink
Thanks, Jeff, that's getting close. Of course, we are left with a conundrum: how can a far-away galaxy be 182 billion light years away in a universe which is 13 billion years old? But then there's lots about physics, at the universal level as well as the sub-atomic one, that's paradoxical. Funny, isn't it? Makes it rather like theology!