When Celsius = Fahrenheit
A while back, someone ended up at a page on this blog by asking Google for "the temperature at which the Celsius scale and Fahrenheit scale are the same number". I don't think they found the answer because I'd never actually discussed that question1, but I thought the question was pretty interesting and discussing the answer might be a bit of good, clean rocket-science fun.
Actually, there is a prior question that I think is interesting, namely: how do we know that there is a temperature where the Celsius and Fahrenheit scales agree? The answer to that question is related to a simple mathematical idea.2 We can picture this mathematical idea by drawing two lines on a chalkboard (or whiteboard) with a rule.
First, draw line A any way you want, but make it more horizontal than vertical, just to keep things clear. Now, draw line B in such a way that it's point farthest left is below line A, but its point farthest right is above line A. What you will always find that that line B and line A will cross at some point. This may seem like an obvious conclusion but it is also a very powerful conclusion. Now, knowing where they will cross is another, often more difficult, question to answer.
How do we know, then, that the Fahrenheit and Celsius lines cross? Well, the freezing point of water, say, on the Celsius scale is 0°C, and on the Fahrenheit it is 32°F. On the other hand, absolute zero is -273.15°C, but -459.67°F. So, at the freezing point of water the Fahrenheit line is above the Celsius line, but at absolute zero that situation is reversed.
Finding the point where they cross is a simple question to answer with algebra. The equation that converts Fahrenheit degrees into Celsius degrees is
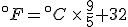
The equation that goes the other way is
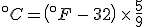
To find the temperature where the two lines cross, take one of the equations and set
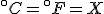
so that
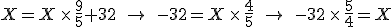
and then solve for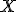 
. The result is that
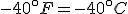
[Addendum: 19 February 2008, for the Kelvin & Fahrenheit folks]
The Kelvin scale of temperatures is a thermodynamic temperature scale: it's zero point is the same as zero temperature in thermodynamic equations. It used Celsius-sized degrees, and there is indeed a temperature at which the Kelvin and Fahrenheit scales cross. The relation between the two is
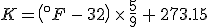
(Note that the absolute temperature scale uses "Kelvins" as the name of the units, and not "degrees Kelvin".) As in the Fahrenheit / Celsius example, set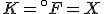 
and solve for 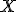, with the result that
As before, Fahrenheit degrees are larger than Kelvins and will eventually overtake them, but the initial difference between the zero points is much larger, so the crossing point is at a much higher temperature.
———-
1Because of the way links on blogs select different combinations of individual posts, by days, by months, by topics, etc., internet search engines often present the least likely links as solutions to unusual word combinations in search strings. I find this phenomenon endlessly fascinating.
2The mathematical idea is one that I've always thought was a "Fundamental Theorem of [some branch of mathematics]", but I've forgotten which (if I ever knew) and haven't been able to identify yet. This is probably another effect of encroaching old-age infirmity.
I imagine — possibly remember — the theorem saying something like:
For a continuous function
defined on the interval
, for
,
takes on all values between
and
.
4 Responses
Subscribe to comments via RSS
Subscribe to comments via RSS
Leave a Reply
To thwart spam, comments by new people are held for moderation; give me a bit of time and your comment will show up.
I welcome comments -- even dissent -- but I will delete without notice irrelevant, rude, psychotic, or incomprehensible comments, particularly those that I deem homophobic, unless they are amusing. The same goes for commercial comments and trackbacks. Sorry, but it's my blog and my decisions are final.
on Thursday, 7 February 2008 at 08.23
Permalink
I'm a bit of a northerner who catches some Canadian radio, so I've mentally used those equations a few times. I often dwell on which scale is "better", F or C. Both are limited when doing calculations for science experiments, but for everyday use it is handier for humans to have a scale with numbers clustered around a zero. Celsius has the advantage of a more world wide standard, but I am partial to Fahrenheit, because of the location of zero.
Zero was initially chosen on the Fahrenheit scale as the point where salt water freezes, but for me zero is the point where outdoor human activity becomes significantly more difficult. Freezing temperatures in general makes things more difficult, but we can usually carry on with modest adjustments, until the temp hits zero F or lower. Motor vehicles in running condition usually start with minor assistance down to zero. After that, the weak start to become apparent. I have a friend who runs a car wash, and he will get customers year around, until the temp drops below zero. Then it is quiet time.
on Thursday, 7 February 2008 at 09.23
Permalink
It's the intermediate value theorem.
on Thursday, 7 February 2008 at 17.15
Permalink
It's the intermediate value theorem.
Well, it would be, wouldn't it.
I think, Fred, that we tend to find it convenient to have smallish numbers measure things that we commonly encounter in everyday human life. Perhaps it's deeply meaningful and has to do with the earliest counting notions of one, two, many….
On the other hand, I think you could find, in time, useful rule-of-thumb correlates for most any arbitrary temperature scale that you commonly used, which is not to say that your sense about Fahrenheit degrees are merely arbitrary.
Personally I prefer to use Kelvins, one Kelvin being the same size as one Celsius degree but 0 K being "absolute zero", so the Kelvin scale is the thermodynamic temperature scale (although the size of the degree remains arbitrary). But, to many, 295 K just sounds hot.
The thing I never really understood during the great metric debate 30 or so years ago was the complaint that the Celsius degree was too big to be useful. On the other hand, I am at peace with fractions and decimal parts.
on Thursday, 7 February 2008 at 19.25
Permalink
I live a little further north than Fred, and am puzzled why anyone (or any country) would persist in using Fahrenheit when Celsius is so much simpler and elegant: water freezes at zero, it boils at 100. Metric rocks! I've become sufficiently used to the Celsius scale (introduced in Canada in the mid-1970s) that when I hear temperatures given on NPR I automatically convert them to Celsius so I know how warm (or cold) it is.
I'd not come across the idea that Fahrenheit used the freezing point of salt water to establish his zero. So you sent me to Wikipedia, the source of all knowledge (accurate as well as spurious). What bothered me is that surely the freezing temperature of salt water depends on the salinity of the solution (just to sound like a scientist, dontcha now): Dead Sea water would presumably freeze at a considerably lower temperature than, say, water in Chesapeake Bay near the mouth of the Susquehanna River, so 0-F as the freezing point of salt water is pretty vague. The Wikipedia article includes this theory as one of eight theories of how Fahrenheit decided on what temperature to call 'zero'. None of them sound particularly convincing.